第9章	回到目录	第11章

---

10.1 研究背景

流言算法

流言算法，从本质上来说是一种特殊的信息交互算法，其研究的主要内容是信息在复杂网络信息交互结构中的传播效率与代价等问题。

---

10.2 系统模型及非合作行为建模

10.2.1 系统建模

多智能体系统模型包含两部分：拓扑模型和节点动力学模型。

本章统一采用无向图。

---

节点动力学模型通常采用一阶或二阶积分器模型。

一阶积分器模型有如下结构：
$$\dot{x}(t)=u(t)\text{\hspace{1em}(10.1)}$$

二阶积分器模型有如下结构：
$$\begin{gathered} \dot{p}(t)=v(t) \\ \dot{v}(t)=u(t)\text{\hspace{1em}(10.2)} \end{gathered}$$

更为一般地，采用线性系统模型描述的节点动力学模型为：
$$\begin{gathered} \dot{x}(t)=Ax(t)+Bu(t) \\ y(t)=Cx(t)\text{\hspace{1em}(10.3)} \end{gathered}$$

---

由于一阶积分器模型有其自身的特殊性秩，本章将单独分节对其进行讨论。

而对于其他节点动力学模型，则统一采用式（10.3）所示的线性系统模型进行描述。

---

在 MAS 的实际运行中，可能存在节点只能获得 相关状态信息 的情况。

含有相关状态信息的节点动力学模型为：

$$\begin{gathered} \dot{x}(t)=Ax(t)+Bu(t) \\ {z}_{ij}(t)=C(x_i(t)-x_j(t))\text{\hspace{1em}(10.4)} \end{gathered}$$

$z_{ij}(t)\in {\mathbb{R}}^p$ 代表节点 $i$ 与邻居 $j$ 之间的相关状态信息。

注意，相关状态信息广泛存在于实际的 MAS 中，其存在并不会影响系统的正常控制，但会对非合作行为检测产生不利影响。

---

10.2.2 非合作行为定义

故障：系统中至少有一项特性或参数偏离了可接受/通常/标准的范围。

在 MAS 中执行故障检测的是节点的邻居而非节点本身，所以即使检测出完整的故障信息也无法对故障进行实时处理。

非合作行为

本章提出非合作行为的概念，即将节点整体视为系统的构成要素，不考虑节点内部具体的运行情况，而只关心其执行任务的能力。若节点无法正常执行协同控制任务，则认定其产生了非合作行为。

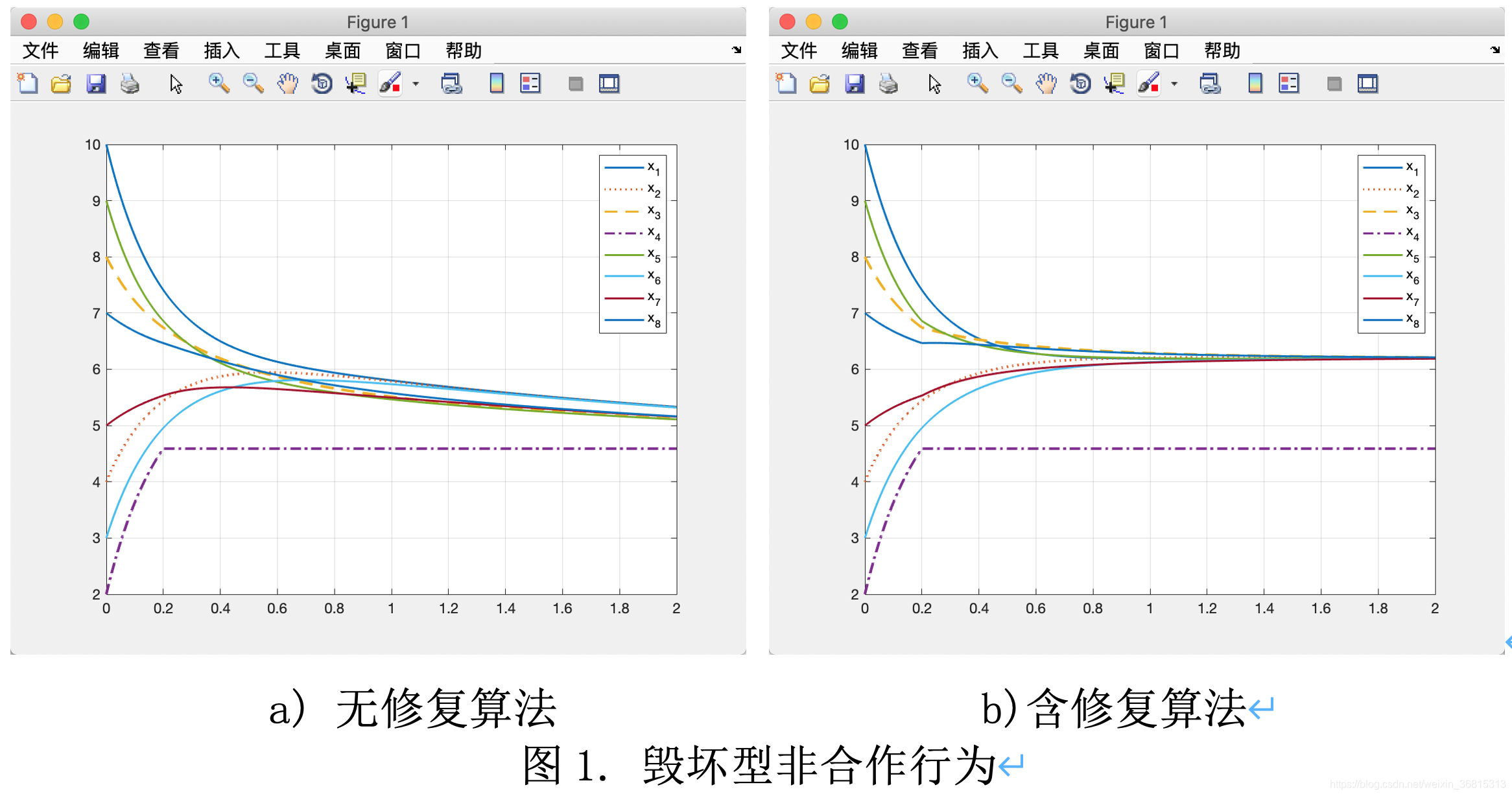
毁坏型

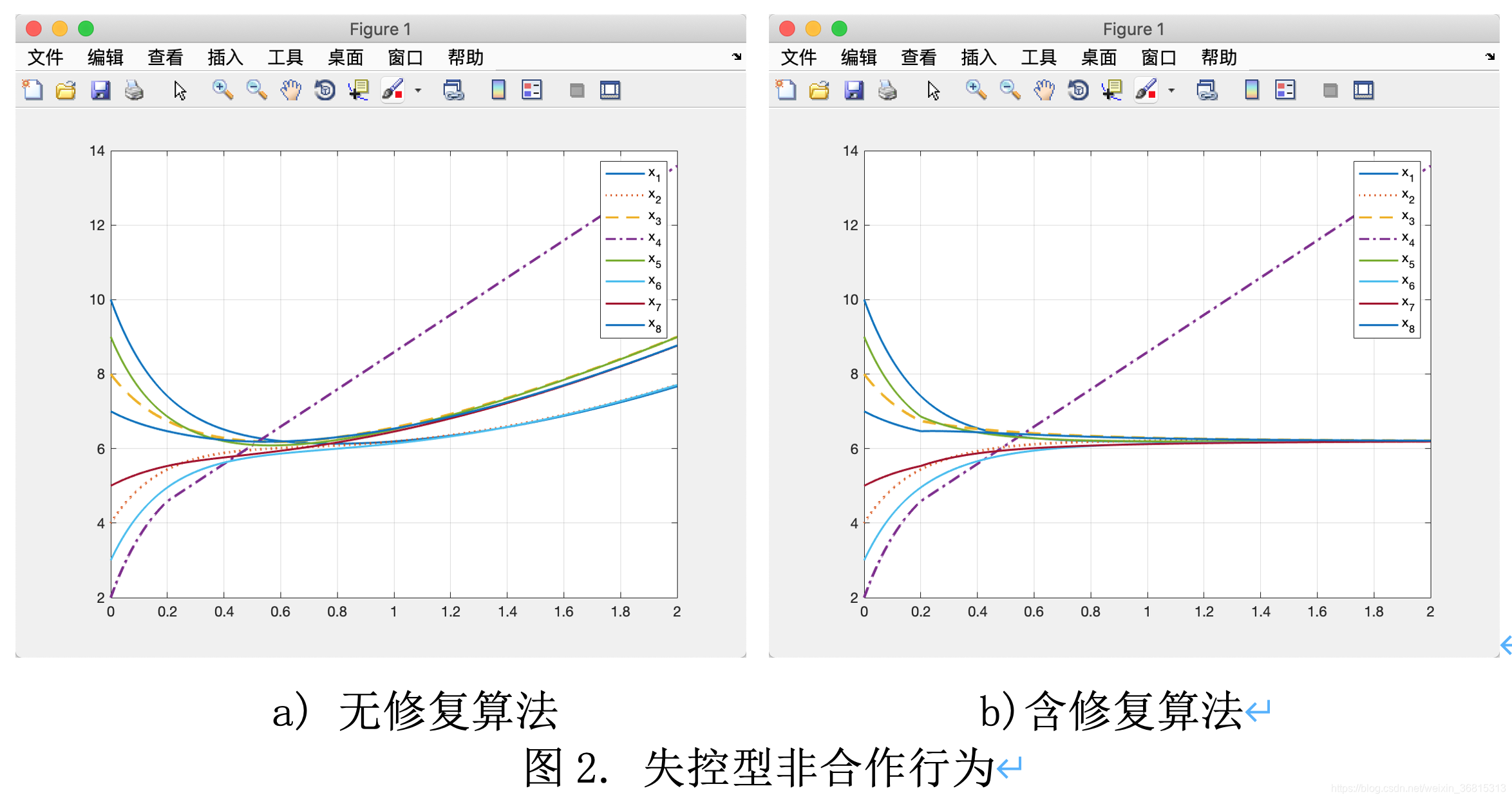
失控型

干扰型

---

10.2.3 非合作行为建模

在故障检测领域，常用的带故障信号的线性系统模型为：
$$\begin{gathered} \dot{x}(t)=Ax(t)+Bu(t)+B_{f}f(t) \\ y(t)=Cx(t)\text{\hspace{1em}(10.5)} \end{gathered}$$

$f(t)\in {\mathbb{R}}^q$ 代表故障信号。

---

在非合作行为检测，由于只关心节点执行任务的情况，而不考虑节点内部的运行情况，因此用以下模型：
$$\begin{gathered} \dot{x}(t)=Ax(t)+Bu(t) \\ y(t)=Cx(t)+e(t)\text{\hspace{1em}(10.6)} \end{gathered}$$

$e(t)\in {\mathbb{R}}^q$ 代表残差信号，用于描述节点的非合作行为。

展开来写：
$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\\ {\dot{x}}_5\\ {\dot{x}}_6\\ {\dot{x}}_7\\ {\dot{x}}_8\end{array}\right]=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\end{array}\right]+\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\\ u_5\\ u_6\\ u_7\\ u_8\end{array}\right]$$

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\\ {\dot{x}}_5\\ {\dot{x}}_6\\ {\dot{x}}_7\\ {\dot{x}}_8\end{array}\right]=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\end{array}\right]+\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\ast (-\left[\begin{array}{cccccccc}{d}_{11}& -a_{12}& -a_{13}& -a_{14}& -a_{15}& -a_{16}& -a_{17}& -a_{18}\\ -a_{21}& d_{22}& -a_{23}& -a_{24}& -a_{25}& -a_{26}& -a_{27}& -a_{28}\\ -a_{31}& -a_{32}& d_{33}& -a_{34}& -a_{35}& -a_{36}& -a_{37}& -a_{38}\\ -a_{41}& -a_{42}& -a_{43}& d_{44}& -a_{45}& -a_{46}& -a_{47}& -a_{48}\\ -a_{51}& -a_{52}& -a_{53}& -a_{54}& d_{55}& -a_{56}& -a_{57}& -a_{58}\\ -a_{61}& -a_{62}& -a_{63}& -a_{64}& -a_{65}& d_{66}& -a_{67}& -a_{68}\\ -a_{71}& -a_{72}& -a_{73}& -a_{74}& -a_{75}& -a_{76}& d_{77}& -a_{78}\\ -a_{81}& -a_{82}& -a_{83}& -a_{84}& -a_{85}& -a_{86}& -a_{87}& d_{88}\end{array}\right])\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\end{array}\right]$$

$$\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\\ y_4\\ y_5\\ y_6\\ y_7\\ y_8\end{array}\right]=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_5\\ x_6\\ x_7\\ x_8\end{array}\right]+\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6\\ e_7\\ e_8\end{array}\right]$$

---

针对上述模型（10.6）。

具体的非合作行为类型如下：

1. 毁坏型：$e(t)=-Cx(t)$，此时 $y(t)=0$。
2. 失控型：$e(t)=\text{const}-Cx(t)$。
3. 干扰型：$e(t)=\text{rand}(t)$。

---

10.3 一阶多智能体系统非合作行为检测、隔离与修复

10.3.1 问题描述

实际的 MAS 中，节点需要对状态信息进行采样，且采样周期不可能无限小，因此采用如下离散时间状态下的节点动力学模型：
$$z_i((k+1)T)=z_i(kT)+u_i(kT)T,i=1,\cdots ,N\text{\hspace{1em}(10.7)}$$

$z_i^k$ 是节点在二维空间中的位置坐标。

---

假定节点的控制器有如下结构：
$$u_i^k=P_i(z_i^k,I_i^k)\text{\hspace{1em}(10.8)}$$

---

记所有非合作节点集合为 $F$，时间步长 $k$ 内节点 $i$ 对节点 $j$ 的检测结果为 $q_{i,j}^k$，满足：
$$q_{i,j}^k=\{\begin{array}{r}0,j\notin F\\ 1,j\in F\end{array}\text{\hspace{1em}(10.9)}$$

---

定义系统对节点的检测结果 为 该节点所有邻居节点对其检测结果的综合，形式如下：
$$Q_i^k=\sum _{j=i_1}^{i_p}{q}_{j,i}^k/p=\frac{{\sum }_{j=i_1}^{i_p}{q}_{j,i}^k}{p}\text{\hspace{1em}(10.10)}$$

---

对于单积分模型，输出反映在节点的连续位移上 $z_i^k-z_i^{k-1}$，
或者说是节点的速率输出 $u_i^k$上。
因此，用 $u_i^k$ 作为计算系统残差信号的性能指标。

残差信号为：
$$r_i^k=u_i^{r,k}-u_i^{a,k}\text{\hspace{1em}(10.11)}$$

其中，
$u_i^{r,k}$ 表示在时间步长 $k$ 内通过控制协议 $P$ 求得的系统理论运动状态；
$u_i^{a,k}$ 表示在时间步长 $k$ 内通过实时测量得到的系统实际运动状态，满足：
$$\begin{gathered} u_i^{r,k}=u_i^k=P_i(z_i^k,I_i^k) \\ {u}_i^{a,k}=h(z_i^{k-1},z_i^k)\text{\hspace{1em}(10.12)} \end{gathered}$$

---

定义 10.1 非合作节点

$$\Vert r_i^k\Vert =\Vert u_i^{r,k}-u_i^{a,k}\Vert \ge \chi (\Vert u_i^{r,k}\Vert ,\delta )\text{\hspace{1em}(10.13)}$$

$\chi (\Vert u_i^{r,k}\Vert ,\delta )$ 为门限函数，一般取
$$\chi (\Vert u_i^{r,k}\Vert ,\delta )={\gamma }_1+{\gamma }_2\Vert u_i^{r,k}\Vert$$

---

10.3.2 非合作行为检测、隔离与修复算法设计

1. 基于通信的非合作行为检测算法

直观地说，该非合作行为检测算法就是通过获得目标节点邻居节点的信息，借助齐次的信息交互协议求得目标节点的理论运动状态，
并将其与探测到的实际运动状态
进行比较，若误差超过一定幅值，则判定节点产生了非合作行为。

---

算法6 一阶多智能体系统非合作行为检测算法

输入：目标节点及其邻居节点的状态信息 $z_j^k、I_j^k$。
输出：节点对节点的非合作行为检测结果 $q_{i,j}^k$。

1. 节点 $i$ 借助信息交互内容 1 和 2 获得节点 $j$ 及其所有邻居节点当前的状态信息 $z_j^k、I_j^k$。
2. 节点 $i$ 借助齐次控制协议 $P$ 及式（10.8）获得节点 $j$ 的控制输入 $u_j^k$。
3. 节点 $i$ 借助式（10.12）求得 $u_j^{r,k}、u_j^{a,k}$。

---

3. 非合作节点的隔离与修复

非合作行为修复的目的就是消除非合作节点在产生非合作行为到被邻居隔离这一段时间内对系统产生的不利影响，保证系统预定的控制目标不会因此产生偏差。

补偿量为：
$$u_{i_{\text{comp}},j}=-\sum _{kT=T_f}^{T_{f_p}}(u_i^k-u_{i\setminus j}^k)\text{\hspace{1em}(10.14)}$$

---

10.3.3 仿真和实验

1. 节点无任何异常，正常运行

% 仿真实验

clear;
clc;

A = [0 1 0 0 0 1 1 1;
     1 0 1 0 0 1 0 1;
     0 1 0 1 1 0 0 1;
     0 0 1 0 1 0 1 1;
     0 0 1 1 0 1 1 0;
     1 1 0 0 1 0 1 0;
     1 0 0 1 1 1 0 0;
     1 1 1 1 0 0 0 0;];
 
D = [4 0 0 0 0 0 0 0;
     0 4 0 0 0 0 0 0;
     0 0 4 0 0 0 0 0;
     0 0 0 4 0 0 0 0;
     0 0 0 0 4 0 0 0;
     0 0 0 0 0 4 0 0;
     0 0 0 0 0 0 4 0;
     0 0 0 0 0 0 0 4;];
 
L = D - A;
 
X0 = [10, 4, 8, 2, 9, 3, 5, 7]';
Xt(:,1) = X0;

epsilon = 0.001;

% 时间参数
tbegin = 0;
tfinal = 2;
dT = 0.001;
T(:,1) = 0; 

% 计算次数
times = (tfinal - tbegin) / dT;


for time = 1:1:times
    Xt(:, time+1) = Xt(:, time) - epsilon * L * Xt(:, time);
    T(:, time+1) = T(:, time) + dT;
end


plot(T(1,:),Xt(1,:),'-', T(1,:),Xt(2,:),':', T(1,:),Xt(3,:),'--', T(1,:),Xt(4,:),'-.',...
     T(1,:),Xt(5,:), T(1,:),Xt(6,:), T(1,:),Xt(7,:), T(1,:),Xt(8,:),...
     'linewidth',1)

legend('x_1', 'x_2', 'x_3', 'x_4', 'x_5', 'x_6', 'x_7', 'x_8');

---

2. 节点出现非合作行为

    % 定义发生非合作行为，时间在 0.2s，此时 time=201
    if time == 201
        L(4,:) = 0;
    end

---

3. 节点的三种非合作行为

    if time >= 201
        Et(4, time) = -Ut(4, time);                       % 毁坏型
        % Et(4, time) = -Ut(4, time) - 0.005;               % 失控型
        % Et(4, time) = -Ut(4, time) - 0.03*(rand-0.5);     % 干扰型
        
        Ut(4, time) = Ut(4, time) + Et(4, time);
    end

---

    if time >= 201
        % Et(4, time) = -Ut(4, time);                       % 毁坏型
        Et(4, time) = -Ut(4, time) - 0.005;               % 失控型
        % Et(4, time) = -Ut(4, time) - 0.03*(rand-0.5);     % 干扰型
        
        Ut(4, time) = Ut(4, time) + Et(4, time);
    end
    Zt(:, time+1) = Zt(:, time) - Ut(:, time);

---

    if time >= 201
        % Et(4, time) = -Ut(4, time);                       % 毁坏型
        % Et(4, time) = -Ut(4, time) - 0.005;               % 失控型
        Et(4, time) = -Ut(4, time) - 0.03*(rand-0.5);     % 干扰型
        
        Ut(4, time) = Ut(4, time) + Et(4, time);
    end

---

4. 节点三种非合作行为及修复

    if time >= 201
        % Et(4, time) = -Ut(4, time);                       % 毁坏型
        % Et(4, time) = -Ut(4, time) - 0.005;               % 失控型
        Et(4, time) = -Ut(4, time) - 0.03*(rand-0.5);     % 干扰型
        
        % 修复        
        U_j(:, time) = epsilon * L_j * Zt(:, time);
        U_Comp(:,time) = -( Ut(:, time) - U_j(:, time) );
        Ut(:, time) = Ut(:, time) + U_Comp(:,time);
        
        Ut(4, time) = Ut(4, time) + Et(4, time);        
    end

其中，干扰型的仿真觉得还是这个更贴切一些

for time = 1:1:times
    % 记录时间刻度
    T(:,  time+1) = T(:, time) + dT;

    % 记录状态
    Ut(:, time) = epsilon * L * Zt(:, time);
    % 定义发生非合作行为，时间在 0.2s，此时 time=201
    if time >= 201
        % Et(4, time) = -Ut(4, time);                       % 毁坏型
        % Et(4, time) = -Ut(4, time) - 0.005;               % 失控型
        Et(4, time) =  - 0.12*(rand-0.5);     % 干扰型
        
        % 修复        
        U_j(:, time) = epsilon * L_j * Zt(:, time);
        U_Comp(:,time) = -( Ut(:, time) - U_j(:, time) );
        Ut(:, time) = Ut(:, time) + U_Comp(:,time);
        
        Ut(4, time) = Ut(4, time) + Et(4, time);        
    end
    
    Zt(:, time+1) = Zt(:, time) - Ut(:, time);
    
end

---

10.4 结论