大模型学习-基础篇(六):LoRA的版本改进
总的来说,LoRA改进的方向主要还是逼近全量微调的结果去努力,无论从权重初始化,梯度下降策略,模型层更新策略等角度出发,本质上都是让新的权重更新趋势拟合全量微调的过程。
系列目录-大模型学习篇
问题场景(Problems)
由于LoRA的效果非常棒,使用起来简单高效。并且这种微调思路易于理解且可解释性很强。因此,基于LoRA原始版本的改进非常多。我们这一章就对LoRA的各种改进版本进行简单的介绍。
本文主要借鉴了苏神的博客和知乎博主的文章。
对齐全量微调!这是我看过最精彩的LoRA改进(一)
对齐全量微调!这是我看过最精彩的LoRA改进(二)
解决方案(Solution)
首先,我们需要对LoRA的操作有一些基本概念,这里我简化了另外一位博主对LoRA中的各种问题的回答,并且做了一些描述上的修改。相信大家快速看完以后,会有很多疑惑,这些问题为什么要那样做?相信让我们带上问题去思考,可以帮助理解和吸收知识。
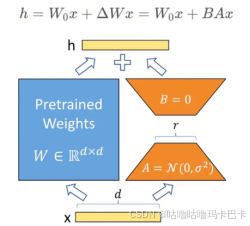
LoRA的主要思想:并行旁路模块,通过低秩分解(先降维再升维)来模拟参数的更新量。
训练时:原模型参数固定,只训练矩阵A和B。
推理时:将BA加到原参数上,不引入额外的推理延迟。
初始化:A采用高斯分布初始化,B初始化为全0,保证训练开始时旁路为0矩阵。
切换任务:当前任务 W 0 + B 1 A 1 W_0+B_1A_1 W0+B1A1,换成 B 2 A 2 B_2A_2 B2A2
特点:将BA加到W上可以消除推理延迟;可插拔不同任务;设计简单效果好。
LoRA的优点
1)一个中心模型服务多个下游任务,节省参数存储量
2)与其它参数高效微调方法正交,可有效组合
3)任务稳定效果好
4)因为适配器权重可以与基本模型合并,不添加任何推理延迟
LoRA的缺点:
参数量不多,百万到千万级别,一般情况下效果能接近全量微调。
1.LoRA权重是否可以合入原模型?:训练后的低秩矩阵 (B*A) 可以与原模型权重相加,得到新的权重。
2.ChatGLM-6B LoRA后的权重多大?:Rank 8, query_key_value下约15M。
3.LoRA微调方法为啥能加速训练?:仅更新部分参数。减少通信时间。支持低精度加速(如FP16、FP8、INT8)。
4.如何在已有LoRA模型上继续训练?:将已有LoRA与base模型合并后继续训练,推荐使用前次训练的数据。
5.LoRA这种微调方法和全参数比起来有什么劣势吗?:相较全参数微调,LoRA训练时间更长,大数据情况下效果不如全参数微调。
6.LORA应该作用于Transformer的哪个参数矩阵?:应将参数平均分配到不同类型权重矩阵(如 Wq 和 Wk),效果最佳。
7.LoRA 微调参数量怎么确定?:由秩 r 和权重矩阵形状决定,目标模块决定参数量。
8.Rank 如何选取?:常见为8,理论效果最佳范围为4-8。
9.alpha参数如何选取?:默认 alpha = rank,简化超参调优。
10.LoRA 高效微调如何避免过拟合?:减小RANK,增大数据集,增加权重衰减或dropout。
11.哪些因素会影响内存使用?:模型大小、批量大小、LoRA参数量、数据集特性。
12.LoRA权重合并?:多套LoRA权重可合并,训练后可简化。
13.是否可以逐层调整LoRA的最优RANK?:可行但复杂,实际中较少使用。
14.Lora的矩阵怎么初始化?:B初始化为0,A正常高斯初始化,避免梯度消失或噪声过大。
LoRA的各种改进版本
VeRA:
研究表明, 预训练好的大语言模型在特定任务上适配时, 模型的"本征维度"很低, 远低于现在LoRA方法的参数规模, 这说明LoRA方法还有进一步优化的空间。
思路:寻求训练参数量更少且能保持相同性能的方法,构造对角矩阵(只有对角线元素非0)减少参数量。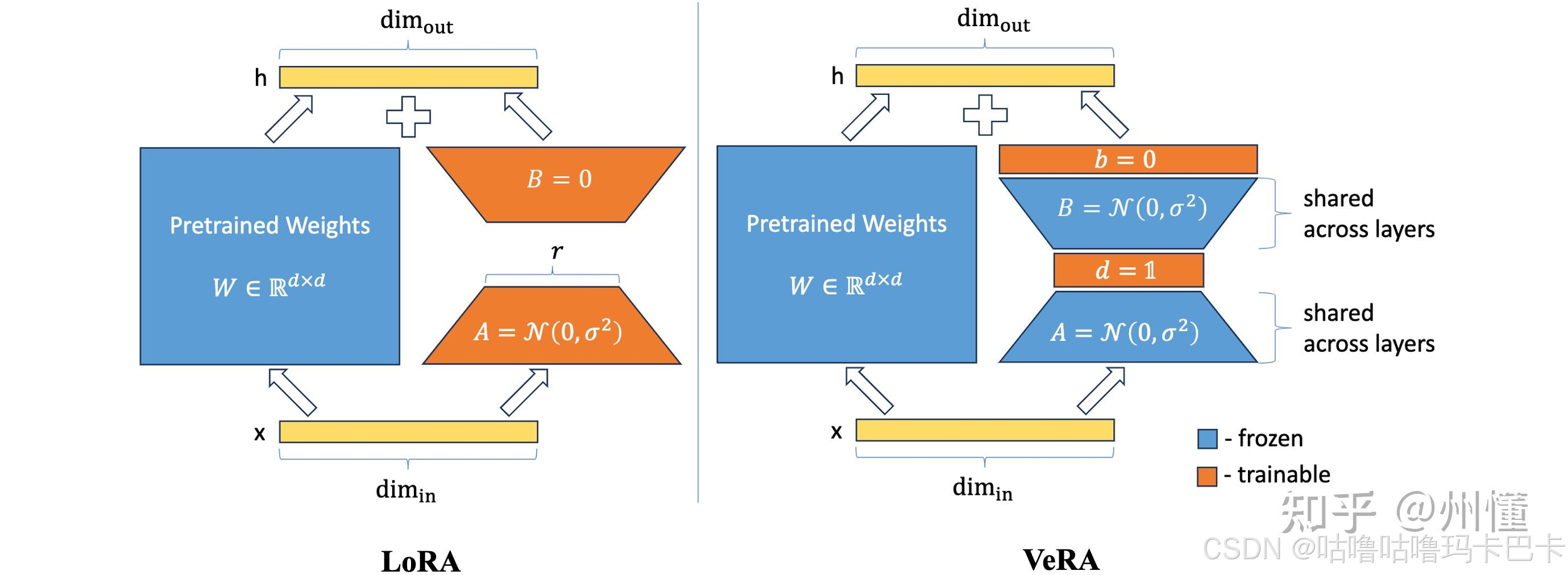
将原始的A和B矩阵进行随机初始化+冻结参数+跨层共享。
初始化策略
共享矩阵:A和B使用Kaiming初始化方法, 通过矩阵的维度对权重值进行缩放, 确保A和B乘积的方差对于不同的秩都能保持一致, 不需要为每个秩去额外调整学习率, 有助于保持权重稳定和训练收敛。
缩放向量: 初始化b为零向量, 这与LoRA初始化B矩阵的方式是类似的, 确保一开始时, 梯度能正常更新。而缩放向量a所有元素都初始化为一个非零值, 从而引入了一个新的超参数。
LISA:
研究表明,LoRA在微调任务中的卓越性能尚未达到在所有设置中普遍超过全参数微调方法。在大规模数据集上连续预训练时,LoRA可训练参数要少得多, 限制了LoRA训练的表达能力。
LoRA的不同层的权重范数具有罕见的倾斜分布,在更新参数时对不同层的重要性程度不同, 权重主要在底层和顶层。作者认为这是LoRA成功的关键之处。
所以,作者使用了Layerwise重要性采样优化方法, 旨在模拟LoRA的更新模式,模拟其快速学习过程,
思路:使用重要性采样方法, 即给定全局学习率, 但中间的层有一定采样概率。如果使用简单的方法,直接给不同层设置不同的学习率, 还是需要一次更新全局模型参数, 效率很低。
DoRA:
由于LoRA与全参数微调方法在模型容量(即可学习的参数规模)上有明显的差距, 在大规模数据上微调,LoRA的效果很多时候比不上全参数微调的方法。因此, 作者深入分析LoRA与FT在更新权重时的差异, 以改进LoRA。
方法:基于权重分解分析(Weight Decomposition Analysis),将预训练权重分解为幅度(magnitude)和方向(direction),分别更新幅度向量和方向矩阵,使得参数更新的梯度下降方向与全量微调近似。
LoRA-GA
针对LoRA-GA的分析,有具体的证明过程,在苏神的博客。我这里简单介绍一下改进的原因何具体思路。
由于LoRA在初始化两个A和B的矩阵以后,我们在优化权重 W 1 W_1 W1时,上一个状态的权重就包含了原始的权重 W 0 W_0 W0以及 A 0 ∗ B 0 A_0*B_0 A0∗B0。但是,如果我们进行全量微调的话,其实就不包括这个 A 0 ∗ B 0 A_0*B_0 A0∗B0。因此,这样就会给未来的权重更新带来一个初始的差值,会影响最终的收敛效果。
因此,我们需要使得 A 0 ∗ B 0 = 0 A_0*B_0=0 A0∗B0=0,因此我们在LoRA中的可以看到需要初始化 A 0 = N ( μ , σ ) A_0=N(\mu,\sigma) A0=N(μ,σ)和 B 0 = 0 B_0=0 B0=0,其实就是这个目的。实际上,我们不需要按这个设置也可以,可以令 A 0 ∗ B 0 = W 0 A_0*B_0=W_0 A0∗B0=W0,再使 W = ( W 0 − A 0 B 0 ) + A B W=(W_0-A_0B_0)+AB W=(W0−A0B0)+AB,实际上也是和原始的方法等效的。
但是,我们既然能保证 W 0 = A 0 B 0 W_0=A_0B_0 W0=A0B0,那么我们还希望 W 1 ≈ A 1 B 1 W_1\approx A_1B_1 W1≈A1B1,因为这样能使LoRA微调更接近全量微调的初始更新状态,所以接近全量微调。经过作者的数学分析,我们其实能够找到一个这样的界,满足我们想要的条件: A 0 = U ( I n ) [ : , : r ] = U [ : , : r ] , B 0 = ( I m ) [ r : 2 r , : ] V = V [ r : 2 r , : ] A0=U(In)[:,:r]=U[:,:r],B0=(Im)[r:2r,:]V=V[r:2r,:] A0=U(In)[:,:r]=U[:,:r],B0=(Im)[r:2r,:]V=V[r:2r,:]
那么这个矩阵,我们是如何取到的呢?
L o R A − G A LoRA-GA LoRA−GA选取一批样本,计算初始梯度 G 0 = ∇ W 0 L G0=∇W0L G0=∇W0L,对梯度 S V D SVD SVD为 G 0 = U Σ V G0=UΣV G0=UΣV,取 U U U的前 r r r列初始化 A A A,取 V V V的第 r + 1 ∼ 2 r r+1∼2r r+1∼2r行初始化 B B B。
总结一下,LoRA-GA是从初始化的角度出发,对于在SGD优化器的条件下,通过改进初始化的LoRA权重,使其更新接近全量微调的结果。但是针对Adam,目前还没有办法对应的优化公式。
LoRA-Pro
从理论上来讲,LoRA-GA只能尽量对齐第一步更新后,那么后面的状态怎么办呢?实际上另外一位作者提出的LoRA-Pro,则从梯度更新的每一步方向上去逼近全量微调,那么最后的结果也许能近似全量微调。
我简单概括一下,LoRA-GA的作者想要需要优化的目标是 argmin A 0 , B 0 ∥ A 0 A 0 ⊤ G 0 + G 0 B 0 ⊤ B 0 − G 0 ∥ F 2 \underset{A_0,B_0}{\operatorname*{argmin}}∥A_0A^⊤_0G_0+G_0B^⊤_0B_0−G_0∥^2_F A0,B0argmin∥A0A0⊤G0+G0B0⊤B0−G0∥F2,LoRA-Pro的作者想要需要优化的目标是 ∥ A t A t ⊤ G t + G t B t ⊤ B t − G t ∥ F 2 ∥A_tA^⊤_tG_t+G_tB^⊤_tB_t−G_t∥^2_F ∥AtAt⊤Gt+GtBt⊤Bt−Gt∥F2,但是我们不可能直接去优化一个由”前向状态“+”优化器策略“共同决定的参数。所以,作者决定直接改SGD优化器,让优化器的更新策略,反过来满足我们想要的结果: argmin H A , t , H B , t ∥ H A , t B t + A t H B , t − G t ∥ F 2 \underset{H_{A,t},H_{B,t}}{\operatorname*{argmin}}∥H_{A,t}B_t+A_tH_{B,t}−G_t∥^2_F HA,t,HB,targmin∥HA,tBt+AtHB,t−Gt∥F2
最后,经过优化后,我们可以得到新的SGD优化器策略是把更新过程中 A , B A,B A,B的梯度 G A , G B G_A,G_B GA,GB换成上面求出的 H A , t H_{A,t} HA,t和 H B , t H_{B,t} HB,t。
当然还有其他LoRA的改进方案,比如stable-LoRA:
W = ( W 0 − s A 0 B 0 ) + s A B W=(W_0−sA_0B_0)+sAB W=(W0−sA0B0)+sAB
其中s作为超参数。
总结(Conclusion)
总的来说,LoRA改进的方向主要还是逼近全量微调的结果去努力,无论从权重初始化,梯度下降策略,模型层更新策略等角度出发,本质上都是让新的权重更新趋势拟合全量微调的过程。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容









所有评论(0)