Diffie-Hellman密钥交换
Diffie-Hellman密钥交换
·
离散对数简介
Diffie-Hellman算法的有效性是依赖于计算离散对数的困难性。
-
对于素数p,若a是其本原根,则
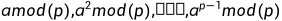 各不相同,且由某个置换中的从1到p-1的整数组成。
各不相同,且由某个置换中的从1到p-1的整数组成。
-
对于任意整数b和素数p的本原根a,我们可以找到唯一的指数,使得
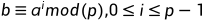 ,指数i称为b的以a为底的模p的离散对数,记为
,指数i称为b的以a为底的模p的离散对数,记为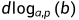 。
。
算法简介
Diffie-Hellman算法的目的是让两个用户安全的交换密钥。
|
Alice和Bob共享一个素数q以及整数a(a<q),其中a是q的本原根 |
|
Alice选择一个随机整数 |
|
Bob选择一个随机整数 |
|
Alice和Bob分别收到对方的公钥 |
|
Alice计算共享密钥 |
|
Bob计算共享密钥 |
Alice和Bob计算的共享密钥值是相同的,至此,双方完成了密钥值交换。
证明:
中间人攻击
Diffie-Hellman算法不能抵抗中间人攻击。
假设Alice和Bob希望交换密钥,而Darth是敌手。则攻击过程如下:
-
Darth首先生成两个随机的私钥
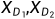 ,并计算相应的公钥
,并计算相应的公钥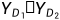
-
Alice将
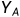 传给Bob
传给Bob
-
Darth截获
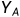 ,将
,将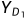 传给Bob,并计算
传给Bob,并计算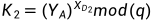
-
Bob收到
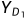 ,计算
,计算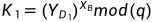
-
Bob将
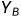 传给Ailce
传给Ailce
-
Darth截获
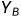 ,将
,将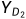 传给Alice,同时计算
传给Alice,同时计算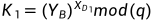
-
Alice收到
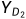 ,计算
,计算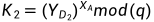
此时,Alice和Bob认为他们共享一个密钥,但实际上,Bob和Darth共享密钥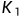 ,Alice和Darth共享密钥
,Alice和Darth共享密钥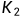 。
。
但这种缺陷可用数字签名和公钥证书来克服。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容

 (
(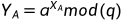
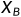 (
(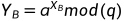
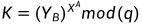
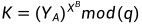





所有评论(0)