Wu X, Mu X. Event-triggered based scaled consensus for multi-agent systems[C]//2019 Chinese Control Conference (CCC). IEEE, 2019: 5544-5549.

1 Introduction

2 Preparation and problem description

2.1 Graph theory

2.2 Problem formulation

$$\begin{array}{rl}{\dot{x}}_i(t)& =u_i(t),i=1,2,\cdots ,N\end{array}\text{\hspace{1em}(1)}$$

3 Centralized approach

$$\begin{array}{rl}{u}_i(t)& =u_i(t_k),\forall t\in [t_k,t_{k+1})\end{array}$$

$$\begin{array}{rl}{u}_i(t)& =\sum _{j\in N_i}{a}_{ij}({\alpha }_{ij}{x}_j(t_k)-x_i(t_k)),\forall t\in [t_k,t_{k+1})\end{array}\text{\hspace{1em}(2)}$$

4 Distributed approach

First, the event triggering time sequence for each agent is denoted as $t_k^i$, $k=0,1,\cdots ,\forall i\in \mathcal{V}$. The measurement error for agent $i$ is defined as:

$$\begin{array}{rl}{e}_i(t)& =x_i(t_k^i)-x_i(t),\forall t\in [t_k^i,t_{k+1}^i)\end{array}\text{\hspace{1em}(10)}$$

Define the relative measurement for agent $i$ as

$$\begin{array}{rl}{z}_i(t)& =\sum _{j\in N_i}{a}_{ij}({\alpha }_{ij}{x}_j(t)-x_i(t))\end{array}\text{\hspace{1em}(12)}$$

distributed control input for agent $i$ is designed as

$$u_i(t)=\sum _{j\in N_i}{a}_{ij}({\alpha }_{ij}{x}_j(t_{k^{\prime }}^j)-x_i(t_k^i))$$

where
$k^{\prime }\triangleq arg{\min }_{l\in {\mathbb{N}}_{+}:t>t_l^j}(t-t_l^j)$.

5 Simulation

5.1 Centralized case

程序 Main_Centralized.m 效果如下

修改程序中不同的 Lambda 值，可以得到以下三种效果。

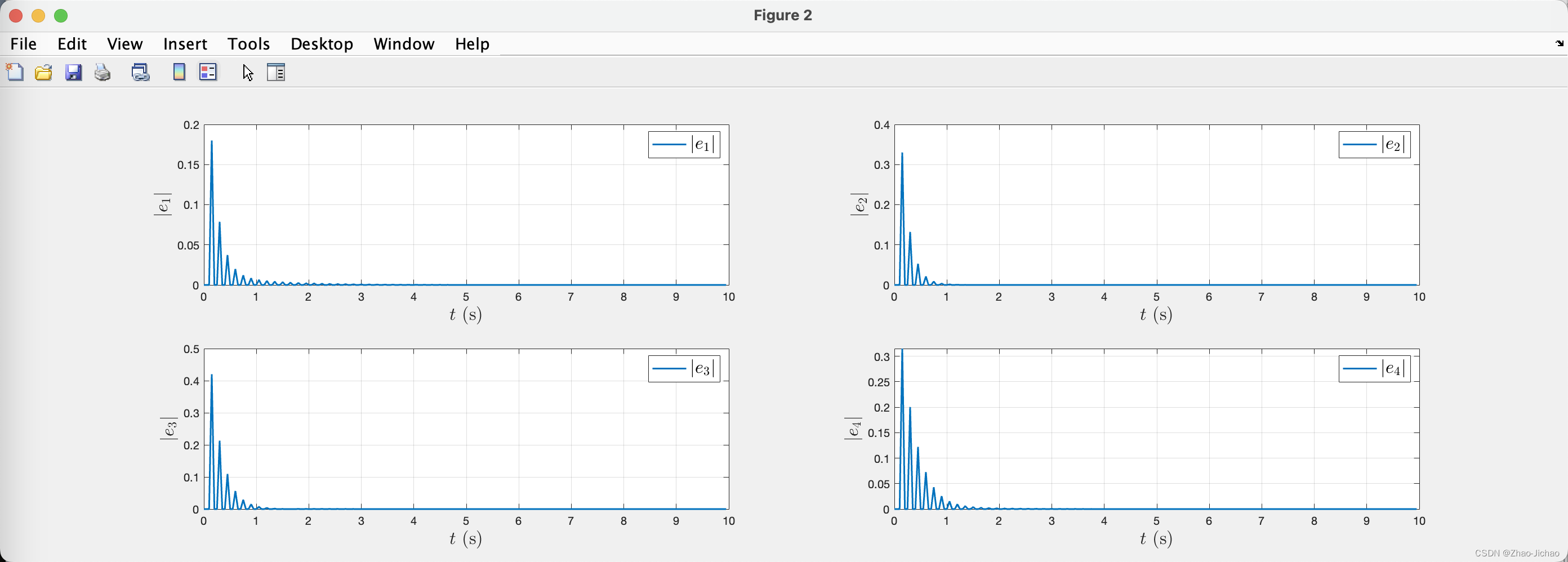
5.2 Distributed case

程序 Main_Distributed.m 效果如下

---

Ref

---

程序有偿，需要代码可加+V：Zhao-Jichao