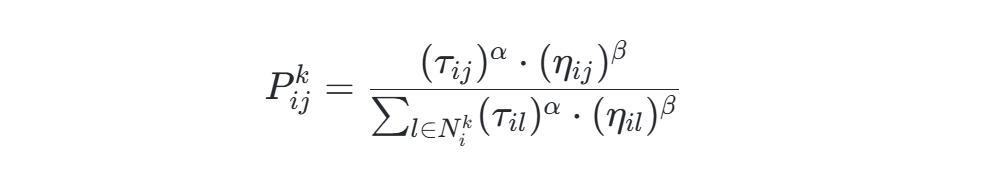
【多智能体系统】基于蚂蚁优化算法、Dijkstra算法、模型预测控制MPC的路径规划与轨迹跟踪算法研究（Matlab代码实现）

💥💥💞💞❤️❤️💥💥博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。⛳️行百里者，半于九十。📋📋📋🎁🎁🎁。

?? G.E.M.

989人浏览 · 2025-02-27 21:08:52

?? G.E.M. · 2025-02-27 21:08:52 发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

⛳️赠与读者

💥1 概述

基于蚂蚁优化算法（ACO）、Dijkstra算法和模型预测控制（MPC）的多智能体系统路径规划与轨迹跟踪研究

一、各算法基本原理及在路径规划与轨迹跟踪中的应用

二、多智能体系统中的协同研究现状

三、关键挑战与未来方向

四、结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

⛳️赠与读者

👨‍💻做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览，免得骤然跌入幽暗的迷宫找不到来时的路，它不足为你揭示全部问题的答案，但若能解答你胸中升起的一朵朵疑云，也未尝不会酿成晚霞斑斓的别一番景致，万一它给你带来了一场精神世界的苦雨，那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。

或许，雨过云收，神驰的天地更清朗.......🔎🔎🔎

💥1 概述

基于蚂蚁优化算法（ACO）、Dijkstra算法和模型预测控制（MPC）的多智能体系统路径规划与轨迹跟踪研究

一、各算法基本原理及在路径规划与轨迹跟踪中的应用

蚂蚁优化算法（ACO）
ACO模拟蚂蚁觅食行为，通过信息素正反馈机制寻找最优路径。其核心步骤包括：
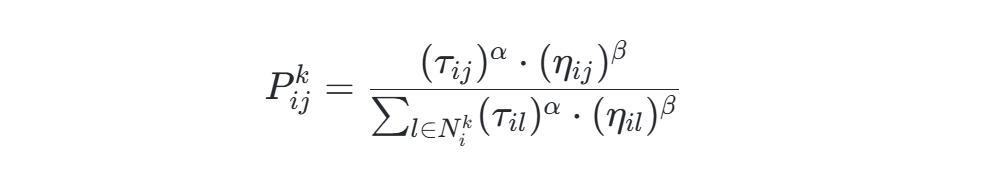
- 路径构建：蚂蚁根据信息素浓度（τijτij）和启发式信息（如距离倒数1/dij1/dij）概率选择路径，公式为：

其中，α和β分别控制信息素与启发式信息的权重。

信息素更新：路径质量越高（如路径更短），信息素增强越多，同时通过蒸发系数ρρ避免局部最优。
应用场景：ACO在机器人路径规划、物流配送（如TSP问题）中表现出色，但需参数调优且计算复杂度随问题规模增大。

Dijkstra算法
Dijkstra算法通过贪心策略寻找单源最短路径，适用于静态环境：
- 流程：初始化节点距离为无穷大，逐步更新最短路径，时间复杂度为O(n2)O(n2)。
- 局限性：无法处理动态障碍物，且在大规模图中效率较低。
- 改进方向：与启发式算法（如A*）或ACO结合，提升动态环境适应性。
模型预测控制（MPC）
MPC基于动态模型滚动优化控制输入，实现轨迹跟踪：
- 核心机制：在每个控制周期内预测未来状态，优化目标函数（如跟踪误差、控制能量）并施加约束（如转向角、速度限制）。
- 优势：鲁棒性强，可处理非线性模型和实时干扰，适用于车辆、无人机等动态轨迹跟踪。
- 挑战：计算复杂度高，需高性能硬件支持。

二、多智能体系统中的协同研究现状

ACO与Dijkstra的混合路径规划
- 策略：Dijkstra快速生成初始路径，ACO优化全局信息素分布，提升搜索效率。例如：

在消防疏散中，Dijkstra提供次优路径作为ACO的初始解，避免ACO早期盲目搜索。
煤矿逃生场景下，混合算法路径长度比A*缩短19%，避障率提升5%。
- 参数优化：通过自适应调整αα、ββ、ρρ等参数，平衡探索与开发能力。

MPC与路径规划算法的集成
- 局部路径规划：MPC结合车辆动力学模型，实时调整路径以避开动态障碍物。例如，无人船通过线性/非线性MPC模型实现高精度轨迹跟踪。
- 多目标优化：将路径长度、安全性、能耗等目标融入MPC代价函数，生成兼顾多约束的轨迹。
- 案例：双轮无人车在MPC控制下，50秒内成功跟踪圆形参考轨迹，转向角收敛至4.13度。
多智能体协同的挑战与解决方案
- 冲突避免：多智能体路径规划（MAPF）需解决顶点冲突（同一时间占用同一节点）和边冲突（路径交叉）。
- 通信限制：动态领导机制（如重新选择领导者）提升密集环境中的协调能力。
- 实时性：采用分布式并行ACO框架（如MPI+OpenMP），384核下实现超线性加速。

三、关键挑战与未来方向

动态环境适应性
- 动态障碍物和实时环境变化要求算法具备快速重规划能力，ACO需与实时传感器数据结合。
- MPC需集成环境预测模型（如DBN威胁评估），提升路径安全性。
算法协调与计算效率
- 混合算法需平衡全局优化（ACO）与局部实时调整（MPC）的冲突，例如分层架构：ACO规划全局路径，MPC处理局部跟踪。
- 并行计算（如GPU加速）和轻量化模型（如深度强化学习）可降低MPC的计算负载。
多目标优化与鲁棒性
- 引入多目标优化框架（如NSGA-II），同时优化路径长度、能耗和冲突风险。
- 强化学习（RL）与ACO结合，通过奖励机制引导多智能体协作。

四、结论

ACO、Dijkstra和MPC在多智能体系统中的协同应用展现了显著潜力：ACO提供全局优化能力，Dijkstra加速初始解生成，MPC确保动态轨迹跟踪。然而，动态环境下的实时性、冲突协调及计算效率仍是核心挑战。未来研究可聚焦于自适应参数调整、分布式架构设计以及跨算法融合（如ACO-MPC深度强化学习框架），以推动多智能体系统在自动驾驶、物流机器人等领域的实用化突破。

📚2 运行结果

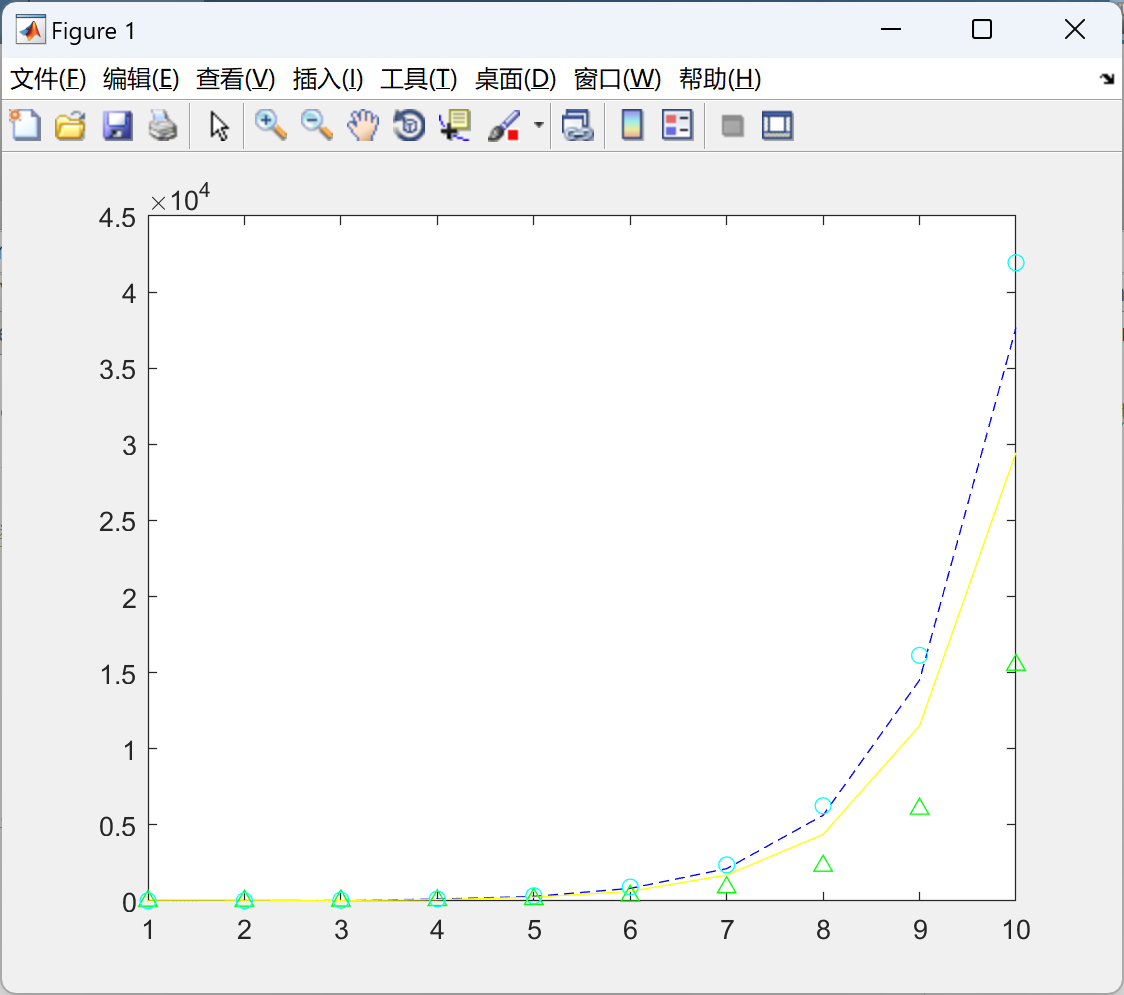
部分代码：

%% 参数设置
Kp = 1.0;
dt = 0.1;
L = 2.9;
max_steer = 60 * pi / 180;
target_v = 40 / 3.6;

%% 轨迹处理
% 定义参考轨迹
refPos_x = path(:, 1);
refPos_y = path(:, 2);
refPos = [refPos_x, refPos_y];

% 计算一阶导数
for i = 1 : length(refPos_x) - 1
    refPos_d(i) = (refPos(i + 1, 2) - refPos(i, 2)) / (refPos(i + 1, 1) - refPos(i, 1));
end
refPos_d(end + 1) = refPos_d(end);

% 计算二阶导数
for i = 2 : length(refPos_x) - 1
    refPos_dd(i) = (refPos(i + 1, 2) - 2 * refPos(i, 2) + refPos(i - 1, 2)) / (0.5*(-refPos(i - 1, 1) + refPos(i, 1))^2 + (refPos(i + 1, 1) - refPos(i, 1))^2);
end
refPos_dd(1) = refPos_dd(2);
refPos_dd(length(refPos_x)) = refPos_dd(length(refPos_x) - 1);

% 计算曲率
for i = 1 : length(refPos_x) - 1
    k(i) = (refPos_dd(i)) / (1 + refPos_d(i)^2)^(1.5);
end

refPos_x = refPos_x';
refPos_y = refPos_y';
refPos_yaw = atan(refPos_d');
refPos_k = k';

%% 绘图
figure
plot(path(:, 1), path(:, 2), 'b');
xlabel('纵向坐标/m');
ylabel('横向坐标/m');
hold on;

%% 主程序
x = 0.1;
y = -0.1;
yaw = 0.1;
v = 0.1;
U = [0.01; 0.01];
pos_actual = [x, y];

ind = 0;
while ind < length(refPos_x)
    % 调节MPC控制器
    [Delta, v, ind, e, U] = MPC_Control(x, y, yaw, refPos_x, refPos_y, refPos_yaw, refPos_k, dt, L, U, target_v);
    
    % 误差太大，退出程序
    if abs(e) > 3
        fprintf('误差过大，退出程序！\n');
       break; 
    end
    
    % 速度P控制器
    a = Kp * (target_v - v);
    
    % 更新状态变量
    [x, y, yaw, v] = updateState(x, y, yaw, v, a, Delta, dt, L, max_steer);
    pos_actual(end + 1, :) = [x, y];
    
    % 画跟踪轨迹图
    plot(x, y, 'ro');
    pause(0.01);
end

%% 保存
path_MPC = pos_actual;
save path_MPC.mat path_MPC;

%% 更新状态变量
%% 算法初始化
% S/U的第一列表示节点编号
% 对于S，第二列表示从源节点到本节点已求得的最小距离，不会更新
% 对于U，第二列表示从源节点到本节点暂时求得的最小距离，可能会更新
S = [4, 0];
U(:, 1) = [1, 2, 3, 5, 6, 7];
U(:, 2) = [inf, inf, 3, 4, inf, inf];

% 最优路径及短暂最优路径的初始化
% 第一列表示节点编号
% 第二列表示从源节点到本节点的路径
path_opt = cell(7, 2);
path_opt(4,:) = {4, 4};
path_temp = cell(7, 2);
path_temp(3,:) = {3, [4, 3]};
path_temp(4,:) = {4, 4};
path_temp(5,:) = {5, [4, 5]};

%% 循环遍历所有节点
while ~isempty(U)
    % 在U集合中找出当前最小距离值及其对应的节点编号，并移除该节点至S集合中
    [distMin, indexMin] = min(U(:, 2));
    nodeMin = U(indexMin, 1);
    S(end+1, :) = [nodeMin, distMin];
    U(indexMin,:) = [];
    
    % 将最小距离节点添加到最优路径集合
    path_opt(nodeMin,:) = path_temp(nodeMin, :);
    
    % 依次遍历最小距离节点的邻近节点，判断是否在U集合中更新邻近节点的距离值
    for i = 1 : length(nodes{nodeMin, 2})
       % 需要判断的节点
       nodeTemp = nodes{nodeMin, 2}(i);
       % 找到U集合中节点nodeTemp的索引值
       indexTemp = find(nodeTemp == U(:, 1));
       % 判断是否更新
       if ~isempty(indexTemp)
           if distMin + nodes{nodeMin, 3}(i) < U(indexTemp, 2)
               U(indexTemp, 2) = distMin + nodes{nodeMin, 3}(i);
               % 更新暂时最优路径
               path_temp{nodeTemp, 1} = nodeTemp;
               path_temp{nodeTemp, 2} = [path_opt{nodeMin, 2}, nodeTemp];
           end
       end
    end
end